Đối với các nhà đầu tư trên thị trường hàng hóa phái sinh, việc hiểu và áp dụng các công cụ phân tích là yếu tố then chốt để thành công. Một trong những công cụ mạnh mẽ nhất chính là hệ số Option Greeks, một tập hợp các chỉ số tài chính được thiết kế để định lượng rủi ro và đo lường độ nhạy của giá một hợp đồng quyền chọn trước các biến số của thị trường. Việc nắm vững các hệ số này không chỉ giúp bạn quản lý rủi ro hiệu quả mà còn mở ra nhiều cơ hội xây dựng chiến lược giao dịch tinh vi trên các sản phẩm như quyền chọn dầu thô, kim loại hay nông sản.

Ứng dụng hệ số Option Greeks trong giao dịch quyền chọn hàng hóa phái sinh

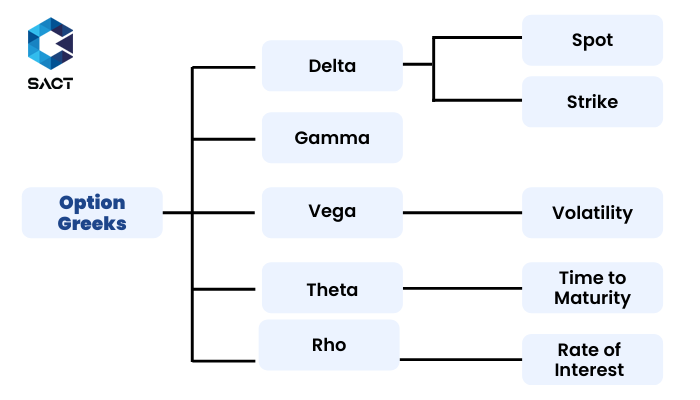
Các giá trị của hệ số Option Greeks về bản chất là động, nghĩa là chúng thay đổi liên tục theo từng diễn biến nhỏ nhất của thị trường. Chúng được tính toán dựa trên mô hình định giá quyền chọn nổi tiếng như Black-Scholes và về mặt toán học, chúng chính là các đạo hàm riêng phần của giá quyền chọn. Bộ công cụ này bao gồm 5 hệ số cốt lõi: Delta, Gamma, Theta, Vega và Rho, mỗi hệ số đại diện cho một loại rủi ro cụ thể.

Ý nghĩa 5 hệ số Option Greeks cốt lõi trong giao dịch hàng hóa

Để áp dụng hiệu quả vào việc giao dịch quyền chọn kim loại, năng lượng hay nông sản, trước hết chúng ta cần hiểu rõ vai trò của từng hệ số trong việc đo lường độ nhạy của hợp đồng.

Delta (Δ): Đo lường rủi ro về hướng giá

Delta là hệ số quan trọng nhất, cho biết giá của một hợp đồng quyền chọn sẽ thay đổi bao nhiêu khi giá của tài sản cơ sở (ví dụ: giá dầu WTI) thay đổi 1 đơn vị. Giá trị của Delta dao động từ 0 đến 1.0 đối với quyền chọn mua (Call option) và từ -1.0 đến 0 đối với quyền chọn bán (Put option). Delta cũng có thể được hiểu gần đúng là xác suất để quyền chọn đáo hạn ở trạng thái có lãi (in-the-money).

Ví dụ, nếu một quyền chọn mua dầu thô có Delta là 0.6, điều này có nghĩa là nếu giá dầu thô tăng 1 USD, giá của quyền chọn mua này sẽ tăng khoảng 0.6 USD. Hiểu rõ Delta là nền tảng cho chiến lược phòng hộ rủi ro (hedging) phổ biến nhất, gọi là “phòng hộ Delta”.

Gamma (Γ): Đo lường sự thay đổi của Delta

Nếu Delta cho bạn biết tốc độ thay đổi của giá quyền chọn, thì Gamma chính là gia tốc. Gamma đo lường tốc độ thay đổi của chính Delta khi giá tài sản cơ sở biến động. Một quyền chọn có Gamma cao nghĩa là Delta của nó rất nhạy với sự thay đổi của giá. Đây là một yếu tố cực kỳ quan trọng khi quản lý rủi ro phi tuyến tính, đặc biệt với các hợp đồng quyền chọn đang ở trạng thái hòa vốn (at-the-money) và gần ngày đáo hạn.

Trong các thị trường hàng hóa vốn biến động mạnh như khí tự nhiên, việc theo dõi Gamma giúp nhà đầu tư dự đoán được mức độ rủi ro của vị thế phòng hộ Delta có thể thay đổi nhanh đến mức nào.

Theta (Θ): Đo lường sự suy giảm giá trị theo thời gian

Theta, hay còn gọi là “hao mòn thời gian”, thể hiện giá trị mà một hợp đồng quyền chọn sẽ mất đi mỗi ngày trôi qua, giả định các yếu tố khác không đổi. Theta luôn là một giá trị âm cho người mua quyền chọn. Đối với người bán quyền chọn, Theta lại là một nguồn lợi nhuận tiềm năng, vì họ thu được phí khi giá trị quyền chọn giảm dần theo thời gian. Các quyền chọn ngắn hạn có mức độ hao mòn Theta nhanh nhất.

Vega (ν): Đo lường rủi ro về sự biến động

Vega đo lường độ nhạy của giá quyền chọn với sự thay đổi 1% trong mức biến động ngụ ý (implied volatility) của tài sản cơ sở. Đây là hệ số cực kỳ quan trọng trong giao dịch quyền chọn hàng hóa, nơi mà các sự kiện như báo cáo tồn kho, thời tiết, hay căng thẳng địa chính trị có thể làm biến động ngụ ý thay đổi đột ngột. Một Vega cao có nghĩa là giá quyền chọn rất nhạy cảm với các kỳ vọng về sự biến động của thị trường trong tương lai.

Rho (ρ): Đo lường rủi ro về lãi suất

Rho đo lường sự thay đổi của giá quyền chọn khi lãi suất phi rủi ro thay đổi 1%. Khi lãi suất tăng, giá quyền chọn mua có xu hướng tăng và giá quyền chọn bán có xu hướng giảm. Mặc dù trong giao dịch quyền chọn ngắn hạn, Rho có tác động nhỏ nhất so với các hệ số trên, nó vẫn là một yếu tố cần xem xét đối với các vị thế dài hạn.

Nâng cao kiến thức: Các hệ số Greeks bậc cao và ứng dụng thực tế

Ngoài 5 hệ số cơ bản, các nhà giao dịch chuyên nghiệp còn sử dụng các hệ số Greeks bậc cao để tinh chỉnh chiến lược và quản lý rủi ro ở mức độ sâu hơn. Việc hiểu thêm về các công cụ này sẽ mang lại cho bạn lợi thế cạnh tranh đáng kể.

• Vanna: Hệ số này đo lường sự thay đổi của Delta khi biến động ngụ ý thay đổi. Nó rất hữu ích để hiểu cách vị thế phòng hộ Delta của bạn sẽ phản ứng khi thị trường trở nên biến động hơn hoặc ít hơn.
• Charm (hay Delta Decay): Đây là hệ số đo lường sự thay đổi của Delta theo thời gian. Khi một hợp đồng quyền chọn ngô sắp đáo hạn, Charm sẽ cho bạn biết vị thế phòng hộ Delta của bạn sẽ thay đổi nhanh như thế nào chỉ sau một đêm.
• Vomma: Đo lường độ nhạy của Vega đối với sự thay đổi của biến động. Nó cho bạn biết Vega sẽ thay đổi nhanh như thế nào khi thị trường trở nên bất ổn, một yếu tố quan trọng cho các nhà giao dịch chuyên về biến động.

Xây dựng chiến lược giao dịch và phòng hộ rủi ro với các hệ số Greeks

Hiểu lý thuyết là một chuyện, nhưng sức mạnh thực sự của các hệ số Greeks nằm ở việc áp dụng chúng để xây dựng các chiến lược giao dịch trung lập với rủi ro, cho phép bạn kiếm lợi nhuận từ các yếu tố khác ngoài hướng đi của giá.

Chiến lược Delta-Neutral

Đây là chiến lược phổ biến nhất, nhằm mục đích tạo ra một danh mục có tổng Delta bằng 0. Khi đó, những biến động nhỏ của giá tài sản cơ sở sẽ không ảnh hưởng đến giá trị tổng thể của danh mục. Điều này cho phép nhà đầu tư tập trung kiếm lợi nhuận từ sự suy giảm thời gian (Theta) hoặc sự thay đổi của biến động (Vega). Ví dụ, một nhà tạo lập thị trường (market maker) trên sàn giao dịch sẽ liên tục thực hiện phòng hộ Delta để giữ cho danh mục của mình an toàn trước biến động giá.

Chiến lược Gamma-Neutral

Chiến lược này tập trung vào việc giữ cho Delta ổn định bằng cách giữ cho tổng Gamma của danh mục gần bằng 0. Điều này đặc biệt hữu ích khi nhà đầu tư muốn duy trì một vị thế phòng hộ Delta ổn định mà không cần phải liên tục điều chỉnh khi giá tài sản cơ sở biến động mạnh.

Chiến lược Vega-Neutral

Chiến lược Vega-Neutral được thiết kế để loại bỏ tác động từ sự thay đổi của biến động ngụ ý. Nhà đầu tư có thể xây dựng một vị thế không bị ảnh hưởng dù thị trường trở nên biến động hơn hay trầm lắng hơn, rất hữu ích khi giao dịch quyền chọn dầu thô quanh thời điểm có các tin tức quan trọng từ OPEC+.

Kết luận

Tóm lại, hệ số Option Greeks là bộ công cụ không thể thiếu để định lượng rủi ro và đo lường độ nhạy trong giao dịch quyền chọn hàng hóa phái sinh. Chúng cung cấp một bức tranh chi tiết về cách một vị thế sẽ phản ứng trước những thay đổi về giá, thời gian, biến động và lãi suất. Việc hiểu rằng các hệ số này luôn động, được tính toán dựa trên mô hình và về bản chất là các đạo hàm toán học sẽ giúp bạn có một nền tảng vững chắc để ra quyết định.

Từ việc phòng hộ Delta đơn giản đến các chiến lược phức tạp hơn như Gamma hay Vega-neutral, việc làm chủ các hệ số Greeks sẽ nâng tầm kỹ năng giao dịch của bạn, giúp bảo vệ vốn và tối ưu hóa lợi nhuận trong thị trường hàng hóa đầy tiềm năng nhưng cũng không ít thách thức.

Để được tư vấn chi tiết về cách áp dụng các hệ số Option Greeks vào chiến lược giao dịch và phòng hộ rủi ro cho danh mục hàng hóa của bạn, hãy liên hệ với đội ngũ chuyên gia của chúng tôi hoặc mở tài khoản giao dịch qua nền tảng SACT TradingPro hiện đại đã có mặt tại Android và IOS ngay hôm nay để bắt đầu trải nghiệm các công cụ phân tích chuyên nghiệp.